冪対象に関する定理 - 空から毛がはえた

定理 $(Y_1 \times Y_2)^{T} \simeq Y_1^{T} \times Y_2^{T}$ を示す

① 射 $h: (Y_1 \times Y_2)^{T} \to Y_1^{T} \times Y_2^{T}$ の定義

評価写像 $e1: T \times (Y_1 \times Y_2)^{T} \to Y_1 \times Y_2$ を使った以下の図式が可換である。 f:id:yabaniyatun:20190119160634p:plain

また、以下の図式も可換である。

f:id:yabaniyatun:20190119160929p:plain

次に、2つの評価写像

$e2: T \times Y_1^{T} \to Y_1$

$e3: T \times Y_2^{T} \to Y_2$

と、以下の2つの可換図式を使って

f:id:yabaniyatun:20190119161659p:plain

2つの射

$\widetilde{p_{Y_1} \circ e1}: (Y_1 \times Y_2)^{T} \to Y_1^{T}$

$\widetilde{p_{Y_2} \circ e1}: (Y_1 \times Y_2)^{T} \to Y_2^{T}$

を定義する。

ここで、以下を可換にする唯一の射を $h$ と定義する。

f:id:yabaniyatun:20190119162250p:plain

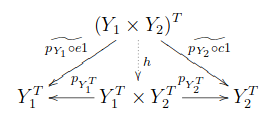
すなわち、

$\widetilde{p_{Y_1} \circ e1} = p_{Y_1^{T}} \circ h$

$\widetilde{p_{Y_2} \circ e1} = p_{Y_2^{T}} \circ h$

が成り立つ。

② 射 $\widetilde{g}: Y_1^{T} \times Y_2^{T} \to (Y_1 \times Y_2)^{T}$ の定義

まず、以下の可換図式が成り立つ。

f:id:yabaniyatun:20190119163833p:plain

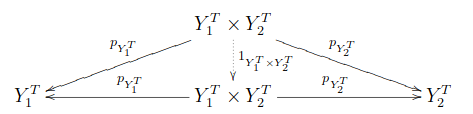
評価写像 $e2$ , $e3$ を使った次の2つの図式も可換。

f:id:yabaniyatun:20190119164101p:plain f:id:yabaniyatun:20190119164143p:plain

ここで、以下を可換にする唯一の射を $g$ と定義する。

f:id:yabaniyatun:20190119164442p:plain

すなわち、

$e2 \circ (1_T \times p_{Y_{1}^{T}}) = p_{Y_1} \circ g$

$e3 \circ (1_T \times p_{Y_{2}^{T}}) = p_{Y_2} \circ g$

が成り立つ。

射 $\widetilde{g}$ を以下の可換図式で定義する。

f:id:yabaniyatun:20190119165248p:plain

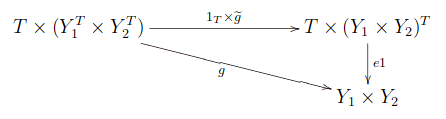
すなわち、

$g = e1 \circ 1_T \times \widetilde{g}$

が成り立つ。

③ $h \circ \widetilde{g}$ の計算

①の最後の2つの式の両辺に、右から $\widetilde{g}$ を掛ける。

$\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}} \circ h \circ \widetilde{g}$

$\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g} = p_{Y_2^{T}} \circ h \circ \widetilde{g}$

これら2つの式から、以下の可換図式が成り立つことがわかる。

f:id:yabaniyatun:20190119170355p:plain

積の普遍性から、2つの式

$\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}}$

$\widetilde{p_{Y_2} \circ e2} \circ \widetilde{g} = p_{Y_2^{T}}$

を示せば、

$h \circ \widetilde{g} = 1_{Y_1^{T} \times Y_2^{T}}$

が言える。

②の最後の3つの式から

$e2 \circ 1_T \times p_{Y_1^{T}} = p_{Y_1} \circ e1 \circ 1_T \times \widetilde{g}$

$e3 \circ 1_T \times p_{Y_2^{T}} = p_{Y_2} \circ e1 \circ 1_T \times \widetilde{g}$

がわかる。

①の3番目、4番目の図式から

$p_{Y_1} \circ e1 = e2 \circ 1_T \times \widetilde{p_{Y_1} \circ e1}$

$p_{Y_2} \circ e1 = e3 \circ 1_T \times \widetilde{p_{Y_2} \circ e1}$

が成り立つので、代入して

$e2 \circ 1_T \times p_{Y_1^{T}} = e2 \circ 1_T \times (\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g})$

$e3 \circ 1_T \times p_{Y_2^{T}} = e3 \circ 1_T \times (\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g})$

評価写像がmonomorphismであることを使うと、上記2つの式から

$\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}}$

$\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g} = p_{Y_2^{T}}$

が成り立つことがわかり、

$h \circ \widetilde{g} = 1_{Y_1^{T} \times Y_2^{T}}$

が示せた。

④ $\widetilde{g} \circ h$ の計算

可換図式

f:id:yabaniyatun:20190119180529p:plain

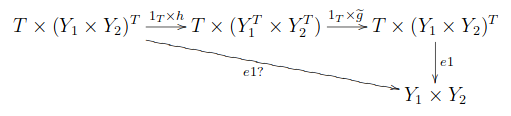
が成り立つこと、すなわち

$e1 \circ 1_T \times (\widetilde{g} \circ h) = e1$

を示せば

$\widetilde{g} \circ h = 1_{(Y_1 \times Y_2)^{T}}$

が言える。

$g = e1 \circ 1_T \times \widetilde{g}$ の右から $1_T \times h$ を掛けて

$g \circ 1_T \times h = e1 \circ 1_T \times (\widetilde{g} \circ h)$

この式の左辺が $e1$ であることを示す。

②の最初の式 $e2 \circ (1_T \times p_{Y_1^{T}}) = p_{Y_1} \circ g$ の右から $1_T \times h$ を掛けて

$e2 \circ 1_T \times (p_{Y_1}^{T} \circ h) = p_{Y_1} \circ g \circ 1_T \times h$

①の最後の式 $\widetilde{p_{Y_1} \circ e1} = p_{Y_1^{T}} \circ h$ から

$e2 \circ 1_T \times \widetilde{p_{Y_1} \circ e1} = p_{Y_1} \circ g \circ 1_T \times h$

①の3番目の図から

$p_{Y_1} \circ e1 = p_{Y_1} \circ g \circ 1_T \times h$ ★

②の2番目の式 $e3 \circ (1_T \times p_{Y_2^{T}}) = p_{Y_2} \circ g$ の右から $1_T \times h$ を掛けて

$e3 \circ 1_T \times (p_{Y_2^{T}} \circ h) = p_{Y_2} \circ g \circ 1_T \times h$

①の最後の式 $\widetilde{p_{Y_2} \circ e1} = p_{Y_2^{T}} \circ h$ から

$e3 \circ 1_T \times \widetilde{p_{Y_2} \circ e1} = p_{Y_2} \circ g \circ 1_T \times h$

①の4番目の図から

$p_{Y_2} \circ e1 = p_{Y_2} \circ g \circ 1_T \times h$ ★

★から、以下の図式において、 $e1 = g \circ 1_T \times h$ が成り立つ。

f:id:yabaniyatun:20190119185853p:plain

よって、 $\widetilde{g} \circ h = 1_{(Y_1 \times Y_2)^{T}}$ が示せた。

おまけ可換図式を書くのに使ったtexソース

\documentclass[12pt]{ujarticle}
\usepackage{amsmath,amsfonts,amsthm,amssymb,amscd}
\usepackage[all]{xy}
\def\objectstyle{\displaystyle}
\begin{document}
\[
\xymatrix@!C=150pt{
  T\times (Y_1\times Y_2)^T \ar[r]^{1_T\times 1_{(Y_1\times Y_2)^T}} \ar[rd]_{e1} & T\times (Y_1\times Y_2)^T \ar[d]^{e1} \\
                                                                                  & Y_1\times Y_2
}
\]
\[
\xymatrix{
  & T \times (Y_1 \times Y_2)^T \ar[ld]_{p_{Y_1} \circ e1} \ar@{.>}[d]^{e1} \ar[rd]^{p_{Y_2} \circ e1} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1 \times Y_2)^T \ar[rd]_{p_{Y_1} \circ e1} \ar[r]^{1_T \times \widetilde{p_{Y_1} \circ e1}} & T \times Y_1^T \ar[d]^{e2} \\
  & Y_1
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1 \times Y_2)^T \ar[rd]_{p_{Y_2} \circ e1} \ar[r]^{1_T \times \widetilde{p_{Y_2} \circ e1}} & T \times Y_2^T \ar[d]^{e3} \\
  & Y_2
}
\]
\[
\xymatrix{
  & (Y_1 \times Y_2)^T \ar[ld]_{\widetilde{p_{Y_1} \circ e1}} \ar@{.>}[d]^{h} \ar[rd]^{\widetilde{p_{Y_2} \circ c1}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix@!C=100pt{
  & Y_1^T \times Y_2^T \ar[ld]_{p_{Y_1^T}} \ar@{.>}[d]^{1_{Y_1^T \times Y_2^T}} \ar[rd]^{p_{Y_2^T}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{e2 \circ (1_T \times p_{Y_1^T})} \ar[r]^{1_T \times p_{Y_1^T}} & T \times Y_1^T \ar[d]^{e2} \\
  & Y_1
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{e3 \circ (1_T \times p_{Y_2^T})} \ar[r]^{1_T \times p_{Y_2^T}} & T \times Y_2^T \ar[d]^{e3} \\
  & Y_2
}
\]
\[
\xymatrix{
  & T \times (Y_1^T \times Y_2^T) \ar[ld]_{e2 \circ (1_T \times p_{Y_1^T})} \ar@{.>}[d]^{g} \ar[rd]^{e3 \circ (1_T \times p_{Y_2^T})} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{g} \ar[r]^{1_T \times \widetilde{g}} & T \times (Y_1 \times Y_2)^T \ar[d]^{e1} \\
  & Y_1 \times Y_2
}
\]
\[
\xymatrix{
  & Y_1^T \times Y_2^T \ar[ld]_{\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g}} \ar@{.>}[d]^{h \circ \widetilde{g}} \ar[rd]^{\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix{
  T \times (Y_1 \times Y_2)^T \ar[rrd]_{e1?} \ar[r]^{1_T \times h} & T \times (Y_1^T \times Y_2^T) \ar[r]^{1_T \times \widetilde{g}} & T \times (Y_1 \times Y_2)^T \ar[d]^{e1} \\
  & & Y_1 \times Y_2
}
\]
\[
\xymatrix@!C=100pt{
  & T \times (Y_1 \times Y_2)^T \ar[ld]_{p_{Y_1} \circ e1} \ar@{.>}[d]^{e1 = g \circ (1_T \times h)} \ar[rd]^{p_{Y_2} \circ e1} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\end{document}