QuantumKatas Superposition Task 12

量子コンピューティングの問題集Microsoft/QuantumKatasでは、Q#プログラムを完成させてユニットテストを実行することにより、問題を解いていくことができます。

今回は、解くのに時間がかかった問題Superposition Task 12について、紹介します。

ユニットテストの実行方法は以下です。(参考: Microsoft Quantum Development Kitのインストール(Linux))

$ cd QuantumKatas/Superposition
$ dotnet test

Task 12

  • 入力
  • ゴール
    • 状態|0...0>から2つのBool型配列が表す等確率の重ね合わせ状態を作る
    • 例) Bool型配列が[false, true, false]と[false, false, true]のとき、(|010> + |001>) / sqrt(2) を作る
  • 前提条件
    • 2つのBool型配列の要素数はどちらもN
    • 2つのBool型配列は、少なくとも1要素は異なる

方針

  1. 最初の量子ビットにアダマールゲートを作用させ、 \frac{|0> + |1>}{\sqrt{2}} \bigotimes |0\cdots 0> = \frac{|0\cdots0> + |1\cdots 0>}{\sqrt{2}}を作る
  2. 上で作ったのは2つの状態の重ね合わせ。すなわち、0番目の量子ビットが|0>の状態Aと|1>の状態Bの重ね合わせ。状態Aに配列bits1、状態Bに配列bits2を設定する。
  3. 1番目〜N-1番目の量子ビットをbits1, bits2の要素に応じて反転させる(|0>を|1>にする)。ここで、0番目の量子ビットの状態を判別のために使う。
  4. 最後に残った0番目の量子ビットを設定する。bits1とbits2は、0番目が異なる場合と、1番目〜N-1番目のどれかが異なる場合があることを考慮する。

解答(テストは通った)

    // Task 12. Superposition of two bit strings
    // Inputs:
    //      1) N qubits in |0...0⟩ state
    //      2) two bit string represented as Bool[]s
    // Goal: create an equal superposition of two basis states given by the bit strings.
    //
    // Bit values false and true correspond to |0⟩ and |1⟩ states.
    // Example: for bit strings [false, true, false] and [false, false, true]
    // the qubit state required is (|010⟩ + |001⟩) / sqrt(2).
    // You are guaranteed that the both bit strings have the same length as the qubit array,
    // and that the bit strings will differ in at least one bit.
    operation TwoBitstringSuperposition (qs : Qubit[], bits1 : Bool[], bits2 : Bool[]) : Unit {
        mutable diffIndex = 0;

        H(qs[0]);

        for (i in 1..Length(qs)-1) {
          if (bits1[i] != bits2[i]) {
            set diffIndex = i;
          }

          if (bits1[i]) {
            (ControlledOnInt(0, X))([qs[0]], qs[i]);
          }

          if (bits2[i]) {
            (ControlledOnInt(1, X))([qs[0]], qs[i]);
          }
        }

        if (diffIndex == 0) {
          if (bits1[0]) {
            X(qs[0]);
          }
        } else {
          if (bits1[0]) {
            if (bits1[diffIndex]) {
              (ControlledOnInt(1, X))([qs[diffIndex]], qs[0]);
            } else {
              (ControlledOnInt(0, X))([qs[diffIndex]], qs[0]);
            }
          }

          if (not bits2[0]) {
            if (bits2[diffIndex]) {
              (ControlledOnInt(1, X))([qs[diffIndex]], qs[0]);
            } else {
              (ControlledOnInt(0, X))([qs[diffIndex]], qs[0]);
            }
          }
        }
    }

ControlledOnInt関数

上記コードではControlledOnInt関数を使いました。

例えば、以下は量子ビットq1, q2, q3が全て状態|1>のとき量子ビットq4にゲートXを作用させます。

 (ControlledOnInt(1, X))([q1, q2, q3], q4);

改良版 (2019/3/31追記)

もっと簡単にできました。ポイントは、状態を識別するための量子ビットを確保して、最後に確保した量子ビットを元に戻すことです。 こちらの記事を参考にさせていただきました。 Microsoft Q# Coding Contest - Winter 2019 - その2 - 純粋関数型雑記帳

    operation TwoBitstringSuperposition (qs : Qubit[], bits1 : Bool[], bits2 : Bool[]) : Unit {
        using (indicator = Qubit()) {
          H(indicator);

          for (i in 0..Length(qs)-1) {
            if (bits1[i]) {
              (ControlledOnInt(0, X))([indicator], qs[i]);
            }

            if (bits2[i]) {
              (ControlledOnInt(1, X))([indicator], qs[i]);
            }
          }

          (ControlledOnBitString(bits2, X))(qs, indicator);
        }
    }

Q#のQuickstartをやってみた

docs.microsoft.com

ファイル構成

  • Bell.qs デバイス側のQ#プログラム。量子ビット(Qubit)に対する操作(operation)を記述。
  • Driver.cs ホスト側のC#プログラム。デバイス側のoperationを呼ぶ。

Bell.qs

namespace Bell {
    open Microsoft.Quantum.Canon;
    open Microsoft.Quantum.Primitive;

    // q1を状態desiredにセットする
    operation Set (desired: Result, q1: Qubit) : Unit {
        // q1の状態を測定(Measurement)
        let current = M(q1);

        if (desired != current) {
          // セットしたい状態と異なる状態ならば反転
          X(q1);
        }
    }

    // countは測定回数。initialはqubits[0]の初期状態。
    operation BellTest (count: Int, initial: Result) : (Int, Int, Int) {
      mutable numOnes = 0;
      mutable agree = 0;
      // 2個のQubitを使う
      using (qubits = Qubit[2]) {
        for (test in 1..count) {
          // qubits[0]を状態initialにセット
          Set(initial, qubits[0]);
          // qubits[1]を|0>にセット
          Set(Zero, qubits[1]);

          // Hはアダマールゲート?
          H(qubits[0]);
          // CNOTゲート?
          CNOT(qubits[0], qubits[1]);
          let res = M(qubits[0]);

          if (M(qubits[1]) == res) {
            set agree = agree + 1;
          }

          // Count the number of ones we saw:
          if (res == One) {
            set numOnes = numOnes + 1;
          }
        }
        Set(Zero, qubits[0]);
        Set(Zero, qubits[1]);
      }

      // Return number of times we saw a |0> and number of times we saw a |1>
      return (count - numOnes, numOnes, agree);
    }
}

Driver.cs

using System;

using Microsoft.Quantum.Simulation.Core;
using Microsoft.Quantum.Simulation.Simulators;

namespace Bell
{
    class Driver
    {
        static void Main(string[] args)
        {
            using (var qsim = new QuantumSimulator())
            {
              // Try initial values
              Result[] initials = new Result[] { Result.Zero, Result.One };
              foreach (Result initial in initials) {
                var res = BellTest.Run(qsim, 1000, initial).Result;
                var (numZeros, numOnes, agree) = res;
                System.Console.WriteLine($"Init:{initial,-4} 0s={numZeros,-4} 1s={numOnes,-4} agree={agree,-4}");
              }
            }

            System.Console.WriteLine("Press any key to continue...");
            Console.ReadKey();
        }
    }
}

実行

$ dotnet run
Init:Zero 0s=508  1s=492  agree=1000
Init:One  0s=470  1s=530  agree=1000
Press any key to continue...

やっていることは、たぶん以下だと思う。

  • 量子ビットを２つ(qubits[0], qubits[1])使う。
  • qubits[0]の初期状態を|0>として、1000回測定した。qubits[0]は|0>が508回、|1>が492回測定された。qubits[0]とqubits[1]は1000回全ての測定で同じ状態だった。
  • qubits[0]の初期状態を|1>として、1000回測定した。qubits[0]は|0>が470回、|1>が530回測定された。qubits[0]とqubits[1]は1000回全ての測定で同じ状態だった。

|0>と|1>の測定回数は実行ごとに変わった。 ゲートHやゲートCNOTが何なのか、不勉強なため、まだわかっていない。

量子コンピューティングのチュートリアル QuantumKatas をやってみようかなぁ。

github.com

C++メモ

コンパイルエラー

$ clang++ test.cpp 
test.cpp:18:6: error: non-const lvalue reference to type 'C' cannot bind to a temporary of type 'C'
  C &c = test();
     ^   ~~~~~~
1 error generated.

上のコンパイルエラーになるソース

#include <cstdio>

class C {
  public:
    C() {}

    void hello() {
      puts("hello");
    }
};

C test() {
  return C();
}

int main(int argc, char* argv[]) {
  C &c = test();
  c.hello();

  return 0;
}

const参照に変更するとコンパイルできる。C::hello()にもconstを付ける。

#include <cstdio>

class C {
  public:
    C() {}

    void hello() const {
      puts("hello");
    }
};

C test() {
  return C();
}

int main(int argc, char* argv[]) {
  const C &c = test();
  c.hello();

  return 0;
}

また、右辺値参照に変更してもコンパイルできる。

#include <cstdio>

class C {
  public:
    C() {}

    void hello() {
      puts("hello");
    }
};

C test() {
  return C();
}

int main(int argc, char* argv[]) {
  C &&c = test();
  c.hello();

  return 0;
}

Microsoft Quantum Development Kitのインストール

環境

$ lsb_release -d
Description:    Ubuntu 18.04.2 LTS

参照サイト

https://docs.microsoft.com/en-us/quantum/install-guide/command-line?view=qsharp-preview

手順

参照サイトに書いてあるとおりにインストールします。

  1. .NET Core SDK 2.0以上(Build Appsの方)を.NET downloads pageからインストール
  2. $ dotnet new -i Microsoft.Quantum.ProjectTemplates を実行

これですべてのインストールが完了。

動作確認

参照サイトに書いてあるとおりに動作確認してみる。

$ git clone https://github.com/Microsoft/Quantum.git
$ cd Quantum/Samples/src/Teleportation/
$ dotnet run
Round 0:    Sent True,  got True.
Teleportation successful!!

Round 1:    Sent False, got False.
Teleportation successful!!

Round 2:    Sent True,  got True.
Teleportation successful!!

Round 3:    Sent False, got False.
Teleportation successful!!

Round 4:    Sent False, got False.
Teleportation successful!!

Round 5:    Sent True,  got True.
Teleportation successful!!

Round 6:    Sent True,  got True.
Teleportation successful!!

Round 7:    Sent True,  got True.
Teleportation successful!!

テレポーテーションのシミュレーションをしているのかなぁ。

vim設定メモ

vim初心者の設定です。

以下を行うための.vimrc

  1. #で→方向に幅を大きくする
  2. "で←方向に幅を小さくする
  3. +で↓方向に高さを大きくする
  4. -で上方向に高さを小さくする
  5. eでファイルツリーを出す

Animated GIF - Find & Share on GIPHYgph.is

set nowritebackup
set nobackup

" vim の矩形選択で文字が無くても右へ進める
set virtualedit=block

" 検索結果をハイライト表示
set hlsearch

set noerrorbells

" タブ文字を CTRL-I で表示し、行末に $ で表示する
set list
" 行末のスペースを可視化
set listchars=tab:^\ ,trail:~

set expandtab
set shiftwidth=2
set showmatch
set smartindent
set noswapfile
set title
set number

syntax on

" netrw設定
" 上部に表示される情報を非表示
let g:netrw_banner = 0
" 表示形式をTreeViewに変更
let g:netrw_liststyle = 3
" 左右分割を右側に開く
let g:netrw_altv = 1
" open in previous window
let g:netrw_browse_split = 4
" 分割で開いたときに20%のサイズで開く
let g:netrw_winsize = 20

nnoremap " <C-w><
nnoremap # <C-w>>
nnoremap - <C-w>-
nnoremap + <C-w>+
nnoremap e :Vexplor<CR>

グラフの圏における冪対象

グラフの圏の対象はグラフである。 Aをエッジ1つの対象、 Dをノード1つの対象とする。 この圏における冪対象 A^{A}, A^{D}, D^{A}, D^{D}はそれぞれどんなグラフだろうか?

A^{A}の形

グラフ Xがどんな形をしているかを調べるためには、まず、射 D \to X, 射 A \to Xがそれぞれ何個あるかを調べる。 また、グラフの圏における終対象 1はノード1つエッジ(ループ)1つのグラフなので、射 1 \to Xの個数が Xが持つループの個数になる。

冪対象の定義から、以下の一対一対応が成り立つ。

\frac{D \to A^{A}}{A \times D \to A}, \frac{A \to A^{A}}{A \times A \to A}

下側の射のdomainは以下のようになる。

A \times D \simeq 2D, A \times A \simeq 2D + A

2D \to Aは4個ある。 2D+A \to Aも4個ある。また A \to Aは1個あるので、ループ 1 \to A^{A}は1個ある。 よって、 A^{A}は4個のノード、4個のエッジ(そのうち1つはループ)のグラフであることがわかる。

A^{A}の4個のエッジ(射 A \times A \to A)を a1, a2, a3 , a4と書こう。

以下のように、 Aのsourceを0, targetを1と書く。 f:id:yabaniyatun:20190211185547p:plain

A \times Aは以下のようになる。

f:id:yabaniyatun:20190211185733p:plain

4個のエッジを以下のように定義する。

ai(0, 0) = 0 (i=1, 2, 3, 4)

ai(1, 1) = 1 (i=1, 2, 3, 4)

a1(0, 1) = 0

a1(0, 1) = 0

a2(0, 1) = 0

a2(1, 0) = 1

a3(0, 1) = 1

a3(1, 0) = 0

a4(0, 1) = 1

a4(1, 0) = 1

ここで以下の2つの射を考える。

1_{A} \times s: A \times D \to A \times A

1_{A} \times t: A \times D \to A \times A

sはノードをエッジのsourceに移す射であり、 tはノードをエッジのtargetに移す射とする。

A \times D \simeq 2D = \{0, 1\}と書くと、以下が成り立つ。

1_{A} \times s (0) = (0, 0)

1{_A} \times s (1) = (1, 0)

1_{A} \times t (0) = (0, 1)

1_{A} \times t (1) = (1, 1)

これらと a1, a2 , a3 a4を合成することで、 A^{A}の形を調べる。

まず、 a1と合成する。

a1 \circ (1_{A} \times s) (0) = 0

a1 \circ (1_{A} \times s) (1) = 0

a1 \circ (1_{A} \times t) (0) = 0

a1 \circ (1_{A} \times t) (1) = 1

よって、エッジ a1は以下のような形をしている。

f:id:yabaniyatun:20190211191853p:plain

次に a2と合成する。

a2 \circ (1_{A} \times s) (0) = 0

a2 \circ (1_{A} \times s) (1) = 1

a2 \circ (1_{A} \times t) (0) = 0

a2 \circ (1_{A} \times t) (1) = 1

よって、エッジ a2は以下のような形をしている。

f:id:yabaniyatun:20190211192239p:plain

続いて a3と合成する。

a3 \circ (1_{A} \times s) (0) = 0

a3 \circ (1_{A} \times s) (1) = 0

a3 \circ (1_{A} \times t) (0) = 1

a3 \circ (1_{A} \times t) (1) = 1

よって、エッジ a3は以下のような形をしている。

f:id:yabaniyatun:20190211192522p:plain

最後に a4と合成する。

a4 \circ (1_{A} \times s) (0) = 0

a4 \circ (1_{A} \times s) (1) = 1

a4 \circ (1_{A} \times t) (0) = 1

a4 \circ (1_{A} \times t) (1) = 1

よって、エッジ a4は以下のような形をしている。

f:id:yabaniyatun:20190211192737p:plain

以上より、グラフ A^{A}は以下の形をしていることがわかった。

f:id:yabaniyatun:20190211193340p:plain

同様にして他のグラフの形もわかる。

A^{D}の形

f:id:yabaniyatun:20190211193904p:plain

D^{A}の形

f:id:yabaniyatun:20190211194041p:plain

D^{D}の形

f:id:yabaniyatun:20190211194153p:plain

冪対象に関する定理

定理 (Y_1 \times Y_2)^{T} \simeq Y_1^{T} \times Y_2^{T} を示す

① 射 h: (Y_1 \times Y_2)^{T} \to Y_1^{T} \times Y_2^{T}の定義

評価写像 e1: T \times (Y_1 \times Y_2)^{T} \to Y_1 \times Y_2を使った以下の図式が可換である。 f:id:yabaniyatun:20190119160634p:plain

また、以下の図式も可換である。

f:id:yabaniyatun:20190119160929p:plain

次に、2つの評価写像

e2: T \times Y_1^{T} \to Y_1

e3: T \times Y_2^{T} \to Y_2

と、以下の2つの可換図式を使って

f:id:yabaniyatun:20190119161659p:plain

2つの射

\widetilde{p_{Y_1} \circ e1}: (Y_1 \times Y_2)^{T} \to Y_1^{T}

\widetilde{p_{Y_2} \circ e1}: (Y_1 \times Y_2)^{T} \to Y_2^{T}

を定義する。

ここで、以下を可換にする唯一の射を hと定義する。

f:id:yabaniyatun:20190119162250p:plain

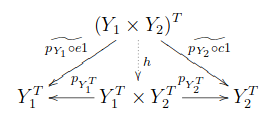
すなわち、

\widetilde{p_{Y_1} \circ e1} = p_{Y_1^{T}} \circ h

\widetilde{p_{Y_2} \circ e1} = p_{Y_2^{T}} \circ h

が成り立つ。

② 射 \widetilde{g}: Y_1^{T} \times Y_2^{T} \to (Y_1 \times Y_2)^{T}の定義

まず、以下の可換図式が成り立つ。

f:id:yabaniyatun:20190119163833p:plain

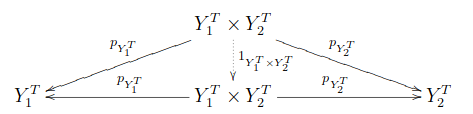
評価写像 e2, e3を使った次の2つの図式も可換。

f:id:yabaniyatun:20190119164101p:plain f:id:yabaniyatun:20190119164143p:plain

ここで、以下を可換にする唯一の射を gと定義する。

f:id:yabaniyatun:20190119164442p:plain

すなわち、

e2 \circ (1_T \times p_{Y_{1}^{T}}) = p_{Y_1} \circ g

e3 \circ (1_T \times p_{Y_{2}^{T}}) = p_{Y_2} \circ g

が成り立つ。

射 \widetilde{g}を以下の可換図式で定義する。

f:id:yabaniyatun:20190119165248p:plain

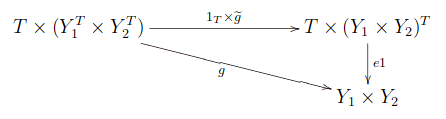
すなわち、

g = e1 \circ 1_T \times \widetilde{g}

が成り立つ。

③ h \circ \widetilde{g}の計算

①の最後の2つの式の両辺に、右から \widetilde{g}を掛ける。

\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}} \circ h \circ \widetilde{g}

\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g} = p_{Y_2^{T}} \circ h \circ \widetilde{g}

これら2つの式から、以下の可換図式が成り立つことがわかる。

f:id:yabaniyatun:20190119170355p:plain

積の普遍性から、2つの式

\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}}

\widetilde{p_{Y_2} \circ e2} \circ \widetilde{g} = p_{Y_2^{T}}

を示せば、

h \circ \widetilde{g} = 1_{Y_1^{T} \times Y_2^{T}}

が言える。

②の最後の3つの式から

e2 \circ 1_T \times p_{Y_1^{T}} = p_{Y_1} \circ e1 \circ 1_T \times \widetilde{g}

e3 \circ 1_T \times p_{Y_2^{T}} = p_{Y_2} \circ e1 \circ 1_T \times \widetilde{g}

がわかる。

①の3番目、4番目の図式から

p_{Y_1} \circ e1 = e2 \circ 1_T \times \widetilde{p_{Y_1} \circ e1}

p_{Y_2} \circ e1 = e3 \circ 1_T \times \widetilde{p_{Y_2} \circ e1}

が成り立つので、代入して

e2 \circ 1_T \times p_{Y_1^{T}} = e2 \circ 1_T \times (\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g})

e3 \circ 1_T \times p_{Y_2^{T}} = e3 \circ 1_T \times (\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g})

評価写像がmonomorphismであることを使うと、上記2つの式から

\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}}

\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g} = p_{Y_2^{T}}

が成り立つことがわかり、

h \circ \widetilde{g} = 1_{Y_1^{T} \times Y_2^{T}}

が示せた。

④ \widetilde{g} \circ hの計算

可換図式

f:id:yabaniyatun:20190119180529p:plain

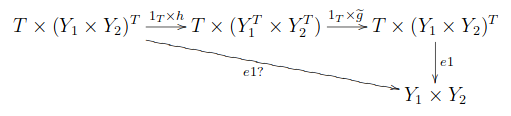
が成り立つこと、すなわち

e1 \circ 1_T \times (\widetilde{g} \circ h) = e1

を示せば

\widetilde{g} \circ h = 1_{(Y_1 \times Y_2)^{T}}

が言える。

g = e1 \circ 1_T \times \widetilde{g}の右から 1_T \times hを掛けて

g \circ 1_T \times h = e1 \circ 1_T \times (\widetilde{g} \circ h)

この式の左辺が e1であることを示す。

②の最初の式 e2 \circ (1_T \times p_{Y_1^{T}}) = p_{Y_1} \circ gの右から 1_T \times hを掛けて

e2 \circ 1_T \times (p_{Y_1}^{T} \circ h) = p_{Y_1} \circ g \circ 1_T \times h

①の最後の式 \widetilde{p_{Y_1} \circ e1} = p_{Y_1^{T}} \circ hから

e2 \circ 1_T \times \widetilde{p_{Y_1} \circ e1} = p_{Y_1} \circ g \circ 1_T \times h

①の3番目の図から

p_{Y_1} \circ e1 = p_{Y_1} \circ g \circ 1_T \times h ★

②の2番目の式 e3 \circ (1_T \times p_{Y_2^{T}}) = p_{Y_2} \circ gの右から 1_T \times hを掛けて

e3 \circ 1_T \times (p_{Y_2^{T}} \circ h) = p_{Y_2} \circ g \circ 1_T \times h

①の最後の式 \widetilde{p_{Y_2} \circ e1} = p_{Y_2^{T}} \circ hから

e3 \circ 1_T \times \widetilde{p_{Y_2} \circ e1} = p_{Y_2} \circ g \circ 1_T \times h

①の4番目の図から

p_{Y_2} \circ e1 = p_{Y_2} \circ g \circ 1_T \times h ★

★から、以下の図式において、 e1 = g \circ 1_T \times hが成り立つ。

f:id:yabaniyatun:20190119185853p:plain

よって、 \widetilde{g} \circ h = 1_{(Y_1 \times Y_2)^{T}}が示せた。

おまけ 可換図式を書くのに使ったtexソース

\documentclass[12pt]{ujarticle}
\usepackage{amsmath,amsfonts,amsthm,amssymb,amscd}
\usepackage[all]{xy}
\def\objectstyle{\displaystyle}
\begin{document}
\[
\xymatrix@!C=150pt{
  T\times (Y_1\times Y_2)^T \ar[r]^{1_T\times 1_{(Y_1\times Y_2)^T}} \ar[rd]_{e1} & T\times (Y_1\times Y_2)^T \ar[d]^{e1} \\
                                                                                  & Y_1\times Y_2
}
\]
\[
\xymatrix{
  & T \times (Y_1 \times Y_2)^T \ar[ld]_{p_{Y_1} \circ e1} \ar@{.>}[d]^{e1} \ar[rd]^{p_{Y_2} \circ e1} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1 \times Y_2)^T \ar[rd]_{p_{Y_1} \circ e1} \ar[r]^{1_T \times \widetilde{p_{Y_1} \circ e1}} & T \times Y_1^T \ar[d]^{e2} \\
  & Y_1
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1 \times Y_2)^T \ar[rd]_{p_{Y_2} \circ e1} \ar[r]^{1_T \times \widetilde{p_{Y_2} \circ e1}} & T \times Y_2^T \ar[d]^{e3} \\
  & Y_2
}
\]
\[
\xymatrix{
  & (Y_1 \times Y_2)^T \ar[ld]_{\widetilde{p_{Y_1} \circ e1}} \ar@{.>}[d]^{h} \ar[rd]^{\widetilde{p_{Y_2} \circ c1}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix@!C=100pt{
  & Y_1^T \times Y_2^T \ar[ld]_{p_{Y_1^T}} \ar@{.>}[d]^{1_{Y_1^T \times Y_2^T}} \ar[rd]^{p_{Y_2^T}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{e2 \circ (1_T \times p_{Y_1^T})} \ar[r]^{1_T \times p_{Y_1^T}} & T \times Y_1^T \ar[d]^{e2} \\
  & Y_1
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{e3 \circ (1_T \times p_{Y_2^T})} \ar[r]^{1_T \times p_{Y_2^T}} & T \times Y_2^T \ar[d]^{e3} \\
  & Y_2
}
\]
\[
\xymatrix{
  & T \times (Y_1^T \times Y_2^T) \ar[ld]_{e2 \circ (1_T \times p_{Y_1^T})} \ar@{.>}[d]^{g} \ar[rd]^{e3 \circ (1_T \times p_{Y_2^T})} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{g} \ar[r]^{1_T \times \widetilde{g}} & T \times (Y_1 \times Y_2)^T \ar[d]^{e1} \\
  & Y_1 \times Y_2
}
\]
\[
\xymatrix{
  & Y_1^T \times Y_2^T \ar[ld]_{\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g}} \ar@{.>}[d]^{h \circ \widetilde{g}} \ar[rd]^{\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix{
  T \times (Y_1 \times Y_2)^T \ar[rrd]_{e1?} \ar[r]^{1_T \times h} & T \times (Y_1^T \times Y_2^T) \ar[r]^{1_T \times \widetilde{g}} & T \times (Y_1 \times Y_2)^T \ar[d]^{e1} \\
  & & Y_1 \times Y_2
}
\]
\[
\xymatrix@!C=100pt{
  & T \times (Y_1 \times Y_2)^T \ar[ld]_{p_{Y_1} \circ e1} \ar@{.>}[d]^{e1 = g \circ (1_T \times h)} \ar[rd]^{p_{Y_2} \circ e1} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\end{document}