2019-03-21

Microsoft Quantum Development Kitのインストール

環境

$ lsb_release -d
Description:    Ubuntu 18.04.2 LTS

参照サイト

https://docs.microsoft.com/en-us/quantum/install-guide/command-line?view=qsharp-preview

手順

参照サイトに書いてあるとおりにインストールします。

.NET Core SDK 2.0以上(Build Appsの方)を.NET downloads pageからインストール
$ dotnet new -i Microsoft.Quantum.ProjectTemplates を実行

これですべてのインストールが完了。

動作確認

参照サイトに書いてあるとおりに動作確認してみる。

$ git clone https://github.com/Microsoft/Quantum.git
$ cd Quantum/Samples/src/Teleportation/
$ dotnet run
Round 0:    Sent True,  got True.
Teleportation successful!!

Round 1:    Sent False, got False.
Teleportation successful!!

Round 2:    Sent True,  got True.
Teleportation successful!!

Round 3:    Sent False, got False.
Teleportation successful!!

Round 4:    Sent False, got False.
Teleportation successful!!

Round 5:    Sent True,  got True.
Teleportation successful!!

Round 6:    Sent True,  got True.
Teleportation successful!!

Round 7:    Sent True,  got True.
Teleportation successful!!

テレポーテーションのシミュレーションをしているのかなぁ。

2019-02-16

vim設定メモ

vim初心者の設定です。

以下を行うための.vimrc

#で→方向に幅を大きくする
"で←方向に幅を小さくする
+で↓方向に高さを大きくする
-で上方向に高さを小さくする
eでファイルツリーを出す

gph.is

set nowritebackup
set nobackup

" vim の矩形選択で文字が無くても右へ進める
set virtualedit=block

" 検索結果をハイライト表示
set hlsearch

set noerrorbells

" タブ文字を CTRL-I で表示し、行末に $ で表示する
set list
" 行末のスペースを可視化
set listchars=tab:^\ ,trail:~

set expandtab
set shiftwidth=2
set showmatch
set smartindent
set noswapfile
set title
set number

syntax on

" netrw設定
" 上部に表示される情報を非表示
let g:netrw_banner = 0
" 表示形式をTreeViewに変更
let g:netrw_liststyle = 3
" 左右分割を右側に開く
let g:netrw_altv = 1
" open in previous window
let g:netrw_browse_split = 4
" 分割で開いたときに20%のサイズで開く
let g:netrw_winsize = 20

nnoremap " <C-w><
nnoremap # <C-w>>
nnoremap - <C-w>-
nnoremap + <C-w>+
nnoremap e :Vexplor<CR>

2019-02-11

グラフの圏における冪対象

グラフの圏の対象はグラフである。 $A$ をエッジ1つの対象、 $D$ をノード1つの対象とする。この圏における冪対象 $A^{A}$ , $A^{D}$ , $D^{A}$ , $D^{D}$ はそれぞれどんなグラフだろうか?

$A^{A}$ の形

グラフ $X$ がどんな形をしているかを調べるためには、まず、射 $D \to X$ , 射 $A \to X$ がそれぞれ何個あるかを調べる。また、グラフの圏における終対象 $1$ はノード1つエッジ(ループ)1つのグラフなので、射 $1 \to X$ の個数が $X$ が持つループの個数になる。

冪対象の定義から、以下の一対一対応が成り立つ。

$\frac{D \to A^{A}}{A \times D \to A}$ , $\frac{A \to A^{A}}{A \times A \to A}$

下側の射のdomainは以下のようになる。

$A \times D \simeq 2D$ , $A \times A \simeq 2D + A$

$2D \to A$ は4個ある。 $2D+A \to A$ も4個ある。また $A \to A$ は1個あるので、ループ $1 \to A^{A}$ は1個ある。よって、 $A^{A}$ は4個のノード、4個のエッジ(そのうち1つはループ)のグラフであることがわかる。

$A^{A}$ の4個のエッジ(射 $A \times A \to A$ )を $a1$ , $a2$ , $a3$ , $a4$ と書こう。

以下のように、 $A$ のsourceを0, targetを1と書く。 f:id:yabaniyatun:20190211185547p:plain

$A \times A$ は以下のようになる。

f:id:yabaniyatun:20190211185733p:plain

4個のエッジを以下のように定義する。

$ai(0, 0) = 0 (i=1, 2, 3, 4)$

$ai(1, 1) = 1 (i=1, 2, 3, 4)$

$a1(0, 1) = 0$

$a2(0, 1) = 0$

$a2(1, 0) = 1$

$a3(0, 1) = 1$

$a3(1, 0) = 0$

$a4(0, 1) = 1$

$a4(1, 0) = 1$

ここで以下の2つの射を考える。

$1_{A} \times s: A \times D \to A \times A$

$1_{A} \times t: A \times D \to A \times A$

$s$ はノードをエッジのsourceに移す射であり、 $t$ はノードをエッジのtargetに移す射とする。

$A \times D \simeq 2D = \{0, 1\}$ と書くと、以下が成り立つ。

$1_{A} \times s (0) = (0, 0)$

$1{_A} \times s (1) = (1, 0)$

$1_{A} \times t (0) = (0, 1)$

$1_{A} \times t (1) = (1, 1)$

これらと $a1$ , $a2$ , $a3$ $a4$ を合成することで、 $A^{A}$ の形を調べる。

まず、 $a1$ と合成する。

$a1 \circ (1_{A} \times s) (0) = 0$

$a1 \circ (1_{A} \times s) (1) = 0$

$a1 \circ (1_{A} \times t) (0) = 0$

$a1 \circ (1_{A} \times t) (1) = 1$

よって、エッジ $a1$ は以下のような形をしている。

f:id:yabaniyatun:20190211191853p:plain

次に $a2$ と合成する。

$a2 \circ (1_{A} \times s) (0) = 0$

$a2 \circ (1_{A} \times s) (1) = 1$

$a2 \circ (1_{A} \times t) (0) = 0$

$a2 \circ (1_{A} \times t) (1) = 1$

よって、エッジ $a2$ は以下のような形をしている。

f:id:yabaniyatun:20190211192239p:plain

続いて $a3$ と合成する。

$a3 \circ (1_{A} \times s) (0) = 0$

$a3 \circ (1_{A} \times s) (1) = 0$

$a3 \circ (1_{A} \times t) (0) = 1$

$a3 \circ (1_{A} \times t) (1) = 1$

よって、エッジ $a3$ は以下のような形をしている。

f:id:yabaniyatun:20190211192522p:plain

最後に $a4$ と合成する。

$a4 \circ (1_{A} \times s) (0) = 0$

$a4 \circ (1_{A} \times s) (1) = 1$

$a4 \circ (1_{A} \times t) (0) = 1$

$a4 \circ (1_{A} \times t) (1) = 1$

よって、エッジ $a4$ は以下のような形をしている。

f:id:yabaniyatun:20190211192737p:plain

以上より、グラフ $A^{A}$ は以下の形をしていることがわかった。

f:id:yabaniyatun:20190211193340p:plain

同様にして他のグラフの形もわかる。

$A^{D}$ の形

f:id:yabaniyatun:20190211193904p:plain

$D^{A}$ の形

f:id:yabaniyatun:20190211194041p:plain

$D^{D}$ の形

f:id:yabaniyatun:20190211194153p:plain

2019-01-19

冪対象に関する定理

定理 $(Y_1 \times Y_2)^{T} \simeq Y_1^{T} \times Y_2^{T}$ を示す

① 射 $h: (Y_1 \times Y_2)^{T} \to Y_1^{T} \times Y_2^{T}$ の定義

評価写像 $e1: T \times (Y_1 \times Y_2)^{T} \to Y_1 \times Y_2$ を使った以下の図式が可換である。 f:id:yabaniyatun:20190119160634p:plain

また、以下の図式も可換である。

f:id:yabaniyatun:20190119160929p:plain

次に、2つの評価写像

$e2: T \times Y_1^{T} \to Y_1$

$e3: T \times Y_2^{T} \to Y_2$

と、以下の2つの可換図式を使って

f:id:yabaniyatun:20190119161659p:plain

2つの射

$\widetilde{p_{Y_1} \circ e1}: (Y_1 \times Y_2)^{T} \to Y_1^{T}$

$\widetilde{p_{Y_2} \circ e1}: (Y_1 \times Y_2)^{T} \to Y_2^{T}$

を定義する。

ここで、以下を可換にする唯一の射を $h$ と定義する。

f:id:yabaniyatun:20190119162250p:plain

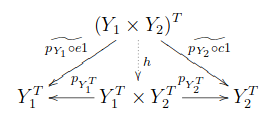
すなわち、

$\widetilde{p_{Y_1} \circ e1} = p_{Y_1^{T}} \circ h$

$\widetilde{p_{Y_2} \circ e1} = p_{Y_2^{T}} \circ h$

が成り立つ。

② 射 $\widetilde{g}: Y_1^{T} \times Y_2^{T} \to (Y_1 \times Y_2)^{T}$ の定義

まず、以下の可換図式が成り立つ。

f:id:yabaniyatun:20190119163833p:plain

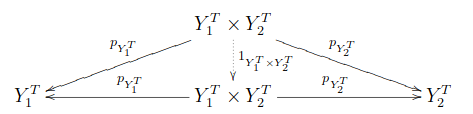
評価写像 $e2$ , $e3$ を使った次の2つの図式も可換。

f:id:yabaniyatun:20190119164101p:plain f:id:yabaniyatun:20190119164143p:plain

ここで、以下を可換にする唯一の射を $g$ と定義する。

f:id:yabaniyatun:20190119164442p:plain

すなわち、

$e2 \circ (1_T \times p_{Y_{1}^{T}}) = p_{Y_1} \circ g$

$e3 \circ (1_T \times p_{Y_{2}^{T}}) = p_{Y_2} \circ g$

が成り立つ。

射 $\widetilde{g}$ を以下の可換図式で定義する。

f:id:yabaniyatun:20190119165248p:plain

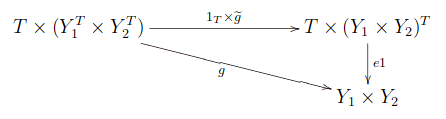
すなわち、

$g = e1 \circ 1_T \times \widetilde{g}$

が成り立つ。

③ $h \circ \widetilde{g}$ の計算

①の最後の2つの式の両辺に、右から $\widetilde{g}$ を掛ける。

$\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}} \circ h \circ \widetilde{g}$

$\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g} = p_{Y_2^{T}} \circ h \circ \widetilde{g}$

これら2つの式から、以下の可換図式が成り立つことがわかる。

f:id:yabaniyatun:20190119170355p:plain

積の普遍性から、2つの式

$\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}}$

$\widetilde{p_{Y_2} \circ e2} \circ \widetilde{g} = p_{Y_2^{T}}$

を示せば、

$h \circ \widetilde{g} = 1_{Y_1^{T} \times Y_2^{T}}$

が言える。

②の最後の3つの式から

$e2 \circ 1_T \times p_{Y_1^{T}} = p_{Y_1} \circ e1 \circ 1_T \times \widetilde{g}$

$e3 \circ 1_T \times p_{Y_2^{T}} = p_{Y_2} \circ e1 \circ 1_T \times \widetilde{g}$

がわかる。

①の3番目、4番目の図式から

$p_{Y_1} \circ e1 = e2 \circ 1_T \times \widetilde{p_{Y_1} \circ e1}$

$p_{Y_2} \circ e1 = e3 \circ 1_T \times \widetilde{p_{Y_2} \circ e1}$

が成り立つので、代入して

$e2 \circ 1_T \times p_{Y_1^{T}} = e2 \circ 1_T \times (\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g})$

$e3 \circ 1_T \times p_{Y_2^{T}} = e3 \circ 1_T \times (\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g})$

評価写像がmonomorphismであることを使うと、上記2つの式から

$\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g} = p_{Y_1^{T}}$

$\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g} = p_{Y_2^{T}}$

が成り立つことがわかり、

$h \circ \widetilde{g} = 1_{Y_1^{T} \times Y_2^{T}}$

が示せた。

④ $\widetilde{g} \circ h$ の計算

可換図式

f:id:yabaniyatun:20190119180529p:plain

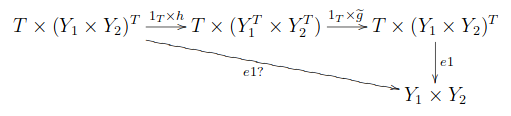
が成り立つこと、すなわち

$e1 \circ 1_T \times (\widetilde{g} \circ h) = e1$

を示せば

$\widetilde{g} \circ h = 1_{(Y_1 \times Y_2)^{T}}$

が言える。

$g = e1 \circ 1_T \times \widetilde{g}$ の右から $1_T \times h$ を掛けて

$g \circ 1_T \times h = e1 \circ 1_T \times (\widetilde{g} \circ h)$

この式の左辺が $e1$ であることを示す。

②の最初の式 $e2 \circ (1_T \times p_{Y_1^{T}}) = p_{Y_1} \circ g$ の右から $1_T \times h$ を掛けて

$e2 \circ 1_T \times (p_{Y_1}^{T} \circ h) = p_{Y_1} \circ g \circ 1_T \times h$

①の最後の式 $\widetilde{p_{Y_1} \circ e1} = p_{Y_1^{T}} \circ h$ から

$e2 \circ 1_T \times \widetilde{p_{Y_1} \circ e1} = p_{Y_1} \circ g \circ 1_T \times h$

①の3番目の図から

$p_{Y_1} \circ e1 = p_{Y_1} \circ g \circ 1_T \times h$ ★

②の2番目の式 $e3 \circ (1_T \times p_{Y_2^{T}}) = p_{Y_2} \circ g$ の右から $1_T \times h$ を掛けて

$e3 \circ 1_T \times (p_{Y_2^{T}} \circ h) = p_{Y_2} \circ g \circ 1_T \times h$

①の最後の式 $\widetilde{p_{Y_2} \circ e1} = p_{Y_2^{T}} \circ h$ から

$e3 \circ 1_T \times \widetilde{p_{Y_2} \circ e1} = p_{Y_2} \circ g \circ 1_T \times h$

①の4番目の図から

$p_{Y_2} \circ e1 = p_{Y_2} \circ g \circ 1_T \times h$ ★

★から、以下の図式において、 $e1 = g \circ 1_T \times h$ が成り立つ。

f:id:yabaniyatun:20190119185853p:plain

よって、 $\widetilde{g} \circ h = 1_{(Y_1 \times Y_2)^{T}}$ が示せた。

おまけ可換図式を書くのに使ったtexソース

\documentclass[12pt]{ujarticle}
\usepackage{amsmath,amsfonts,amsthm,amssymb,amscd}
\usepackage[all]{xy}
\def\objectstyle{\displaystyle}
\begin{document}
\[
\xymatrix@!C=150pt{
  T\times (Y_1\times Y_2)^T \ar[r]^{1_T\times 1_{(Y_1\times Y_2)^T}} \ar[rd]_{e1} & T\times (Y_1\times Y_2)^T \ar[d]^{e1} \\
                                                                                  & Y_1\times Y_2
}
\]
\[
\xymatrix{
  & T \times (Y_1 \times Y_2)^T \ar[ld]_{p_{Y_1} \circ e1} \ar@{.>}[d]^{e1} \ar[rd]^{p_{Y_2} \circ e1} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1 \times Y_2)^T \ar[rd]_{p_{Y_1} \circ e1} \ar[r]^{1_T \times \widetilde{p_{Y_1} \circ e1}} & T \times Y_1^T \ar[d]^{e2} \\
  & Y_1
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1 \times Y_2)^T \ar[rd]_{p_{Y_2} \circ e1} \ar[r]^{1_T \times \widetilde{p_{Y_2} \circ e1}} & T \times Y_2^T \ar[d]^{e3} \\
  & Y_2
}
\]
\[
\xymatrix{
  & (Y_1 \times Y_2)^T \ar[ld]_{\widetilde{p_{Y_1} \circ e1}} \ar@{.>}[d]^{h} \ar[rd]^{\widetilde{p_{Y_2} \circ c1}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix@!C=100pt{
  & Y_1^T \times Y_2^T \ar[ld]_{p_{Y_1^T}} \ar@{.>}[d]^{1_{Y_1^T \times Y_2^T}} \ar[rd]^{p_{Y_2^T}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{e2 \circ (1_T \times p_{Y_1^T})} \ar[r]^{1_T \times p_{Y_1^T}} & T \times Y_1^T \ar[d]^{e2} \\
  & Y_1
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{e3 \circ (1_T \times p_{Y_2^T})} \ar[r]^{1_T \times p_{Y_2^T}} & T \times Y_2^T \ar[d]^{e3} \\
  & Y_2
}
\]
\[
\xymatrix{
  & T \times (Y_1^T \times Y_2^T) \ar[ld]_{e2 \circ (1_T \times p_{Y_1^T})} \ar@{.>}[d]^{g} \ar[rd]^{e3 \circ (1_T \times p_{Y_2^T})} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\[
\xymatrix@!C=150pt{
  T \times (Y_1^T \times Y_2^T) \ar[rd]_{g} \ar[r]^{1_T \times \widetilde{g}} & T \times (Y_1 \times Y_2)^T \ar[d]^{e1} \\
  & Y_1 \times Y_2
}
\]
\[
\xymatrix{
  & Y_1^T \times Y_2^T \ar[ld]_{\widetilde{p_{Y_1} \circ e1} \circ \widetilde{g}} \ar@{.>}[d]^{h \circ \widetilde{g}} \ar[rd]^{\widetilde{p_{Y_2} \circ e1} \circ \widetilde{g}} & \\
  Y_1^T & Y_1^T \times Y_2^T \ar[l]_{p_{Y_1^T}} \ar[r]^{p_{Y_2^T}} & Y_2^T
}
\]
\[
\xymatrix{
  T \times (Y_1 \times Y_2)^T \ar[rrd]_{e1?} \ar[r]^{1_T \times h} & T \times (Y_1^T \times Y_2^T) \ar[r]^{1_T \times \widetilde{g}} & T \times (Y_1 \times Y_2)^T \ar[d]^{e1} \\
  & & Y_1 \times Y_2
}
\]
\[
\xymatrix@!C=100pt{
  & T \times (Y_1 \times Y_2)^T \ar[ld]_{p_{Y_1} \circ e1} \ar@{.>}[d]^{e1 = g \circ (1_T \times h)} \ar[rd]^{p_{Y_2} \circ e1} & \\
  Y_1 & Y_1 \times Y_2 \ar[l]_{p_{Y_1}} \ar[r]^{p_{Y_2}} & Y_2
}
\]
\end{document}

2019-01-15

texインストールメモ

以下の記事を参考にさせていただきました。ありがとうございます。

texliveをインストールしました。圏論の可換図式を書くためのライブラリxy-picは、texliveに含まれているため、すぐ使えました。

$ lsb_release -d
Description:    Ubuntu 18.04.1 LTS
$ sudo apt install texlive-lang-japanese
$ sudo apt install texlive-fonts-recommended
$ sudo apt install texlive-fonts-extra
$ sudo apt install xdvik-ja
$ sudo apt install gv
$ cat test.tex
\documentclass[12pt]{ujarticle}
\usepackage{amsmath,amsfonts,amsthm,amssymb,amscd}
\usepackage[all]{xy}
\def\objectstyle{\displaystyle}
\begin{document}
\[
\xymatrix{
  A \ar[r] \ar[rrd] & B & \ar[d] \\
  C \ar[u] & A \ar[l] \ar[lu] & D
}
\]
\end{document}
$ uplatex test.tex　
$ dvipdfmx test.dvi
$ firefox test.pdf

f:id:yabaniyatun:20190115230900p:plain

2019-01-04

Conceptual Mathematics, Session29, Exercise1

対角線定理(Diagonal Theorem)

積を持つ圏で考える。

対象 $Y$ が以下の命題1を満たすならば、任意のendomap $\alpha: Y \to Y$ は少なくとも１つの不動点を持つ。すなわち、 $\alpha \circ y0 = y0$ を満たす点 $y0: 1 \to Y$ が存在する。

命題1

射 $f: T \times T \to Y$ が任意の射 $g: T \to Y$ をパラメタライズできるような対象 $T$ を持つ。すなわち、 $g(t) = f(t, t0)$ と表せるような点 $t0: 1 \to T$ が存在する。

対角線定理の証明

$Y, T, f, \alpha$ が与えられており、以下の図式が可換であると仮定する。このとき、 $\alpha: Y \to Y$ が不動点を持つことを示す。

$\require{AMScd} \begin{CD} T \times T @>{f}>> Y\\ @A{\delta}AA @VV{\alpha}V\\ T @>>{g}> Y \end{CD}$

ここで $\delta$ は対角写像 $\delta: t \mapsto (t, t)$ である。

図式が可換であることから、任意の点 $t: 1 \to T$ に対して

$g(t) =\alpha(f(t, t))$

が成り立つ。

また、 $f$ は $g$ をパラメタライズできるので、

$g(t) = f(t, t0)$

を満たす点 $t0: 1 \to T$ が存在する。

$t$ に $t0$ を代入すると

$g(t0) = f(t0, t0) = \alpha(f(t0, t0))$

となり、 $\alpha: Y \to Y$ が不動点 $f(t0, t0)$ を持つことが示せた。

対角線定理拡張版

Session29, Exercise1 (p.306)は、対角線定理を少し拡張した以下の定理を示すという問題である。

射 $f: T \times T \to Y$ が任意の射 $T \to Y$ を"弱く"パラメタライズできる(weakly parameterize)ならば、任意のendomap $\alpha: Y \to Y$ は不動点を持つ。

"弱くパラメタライズする"の意味

射 $f: T \times T \to Y$ が任意の射 $g: T \to Y$ を弱くパラメタライズするとは、任意の射 $g$ に対して点 $t0: 1 \to T$ が存在し、可換図式1の $\xi$ が可換図式2を満たすことである。

可換図式1

$\require{AMScd} \begin{CD} T @= T\\ @V{\xi}VV @VV{1_T}V\\ T \times T @>{p_1}>> T \end{CD}$

$\require{AMScd} \begin{CD} T @= T\\ @V{\xi}VV @VV{c}V\\ T \times T @>{p_2}>> T \end{CD}$

$c$ は定値写像であり、任意の $t$ に対して $c(t) = t0$ 。

可換図式2

$\require{AMScd} \begin{CD} 1 @>{t}>> T @>{f \circ \xi}>> Y\\ @| @| @|\\ 1 @>{t}>> T @>{g}>> Y \end{CD}$

$t$ は任意の点。

対角線定理拡張版の証明

可換図式2の $g$ として対角写像 $\delta$ と $f$ とendomap $\alpha$ の合成 $\alpha \circ f \circ \delta$ を選ぶ。以下の図式において、 $\alpha \circ f \circ \delta \circ t = f \circ \xi \circ t$ が成り立つ。

$\require{AMScd} \begin{CD} 1 @>{t}>> T @>{\delta}>> T \times T @>{f}>> Y @>{\alpha}>> Y \end{CD}$

$t$ は任意の点。

$f \circ \xi \circ t$ を $f(t, t\xi)$ と書くと、

$\alpha(f(t, t)) = f(t, t\xi)$

が成り立ち、 $t$ に $t\xi$ を代入すると

$\alpha(f(t\xi, t\xi)) = f(t\xi, t\xi)$

となるので、 $f(t\xi, t\xi)$ が $\alpha: Y \to Y$ の不動点となることが示せた。

メモ

amscdだと、斜めの矢印、左矢印、破線矢印が書けなかった
XyJax を使おうとしたけど、はてなブログでの使い方がわからなかった https://github.com/sonoisa/XyJax
[tex: f(t_{\xi}, t_{\xi})]が表示されなくて困った。t\xiをt_{\xi}の代わりに使った。tex苦手なので間違っているかも。

2019-01-04

MathJaxのテスト

デフォルトでMathJaxに対応していたようだ。ヘッダに何も指定していない。

文中の式。

ラグランジュ方程式は $\frac{d}{dt}\left(\frac{\partial L}{\partial \dot{q}}\right)-\frac{\partial L}{\partial q} = 0$ です。

可換図式も書けた。\\を\\\に変えたら改行されるようになった。

$\require{AMScd} \begin{CD} A @>{f}>> B\\ @V{gg}VV {\large\circlearrowleft} @VV{hh}V\\ C @>>{k}> D \end{CD}$

環境

参照サイト

手順

動作確認

の形

の形

の形

の形

定理 を示す

① 射の定義

② 射の定義

③ の計算

④ の計算

おまけ 可換図式を書くのに使ったtexソース

対角線定理(Diagonal Theorem)

命題1

対角線定理の証明

対角線定理拡張版

"弱くパラメタライズする"の意味

可換図式1

可換図式2

対角線定理拡張版の証明

メモ

$A^{A}$ の形

$A^{D}$ の形

$D^{A}$ の形

$D^{D}$ の形

定理 $(Y_1 \times Y_2)^{T} \simeq Y_1^{T} \times Y_2^{T}$ を示す

① 射 $h: (Y_1 \times Y_2)^{T} \to Y_1^{T} \times Y_2^{T}$ の定義

② 射 $\widetilde{g}: Y_1^{T} \times Y_2^{T} \to (Y_1 \times Y_2)^{T}$ の定義

③ $h \circ \widetilde{g}$ の計算

④ $\widetilde{g} \circ h$ の計算

おまけ可換図式を書くのに使ったtexソース